This is not really ready for explainer-level yet. You should understand derivatives and antiderivatives for this text, i.e.:

• \(\frac{d}{dx}\left(x^{3}+x^{2}\right)=3x^{2}+2x\)
• \(\int_{ }^{ }\left(x^{2}+x\right)dx=\frac{x^{3}}{3}+\frac{x^{2}}{2}\)

Usually, integration / derivatives only go up/down a single degree (so, you're swapping roots and extrema).

In this document, by updating coefficients and the locator, we "cast" roots at any derivative level (e.g., all the extrema or roots) into any other derivative "root group" having enough "slots" to hold the cast -- including casts back into the same polynomial degree.

All we need is Pascal's Triangle diagonals and the ability to move the locator (see previous post).

In pictures, this is what I mean. The blue function is a quintic, and I am directly "casting" its two quadratic (third-derivative) roots to the extrema of a quintic, quartic and cubic.

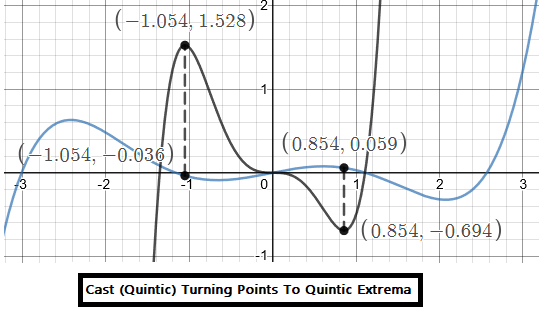
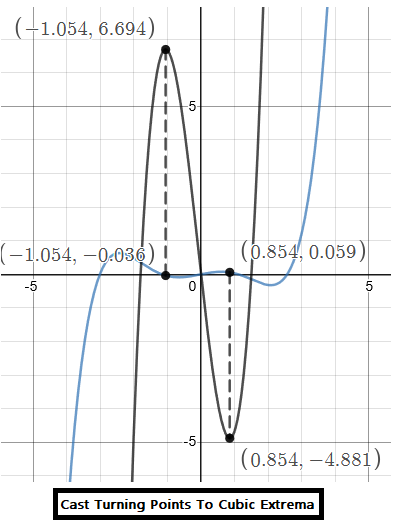TODO: LaTeX: The above were done with fractions: (10,4,1 / 5,4,3), (10,4,1 / 4,3,2) and (10,4,1 / 3,2,1) respectively.

.... TODO: Err...quintics traditionally have 3 turning points, and 2 of whatever it's called above that. I mislabeld the images.

Multiple derivatives and integrals can be combined into one step using Pascal's Triangle diagonals.

Here we have a quintic equation:
\(x^{5}+2x^{4}+-x^{3}-2x^{2}+x+1\)

Its derivative and an equivalent are:
\(\left(5\right)x^{4\ }+\ \left(4\right)2x^{3}-\left(3\right)x^{2}-\left(2\right)2x^{1}+\left(1\right)1\)
\(\left(\frac{5}{1}\right)x^{4}+\left(\frac{4}{1}\right)2x^{3}-\left(\frac{3}{1}\right)x^{2}-\left(\frac{2}{1}\right)2x^{1}+\left(\frac{1}{1}\right)1\)

The fractions can be constructed from Pascal's Triangle diagonals: \(\frac{5,\ 4,\ 3,\ 2,\ 1}{1,\ 1,\ 1,\ 1,\ 1}\) under the operation "extrema" to "roots".



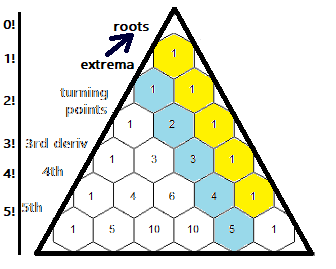
We can also take the second derivative in one step: ...TODO: WIP

---

Footnote: While there is a snag in one cast type (i.e., when casting roots to extrema within the same degree, the y-line at the locator is taken as the casting level, and all "won't fit" roots get cast to the new locator (collapsing the won't-fits to a multi-root). This means that to solve a quintic, e.g., by casting roots to extrema and then deriving, you'd first have to have the locator at a root (so...why wouldn't you just factor then?). I think parabolic (etc) upcasts might work by making the locator "line" itself a polynomial...(I have hints here)...but ultimately my hope is that by describing this expansion to calculus, someone can help / find a way.

You may have noticed that the quadratic-root and cubic-extrema equations differ by only two numbers:

\[x = {-b \pm \sqrt{b^2-{\color{orange}4}ac} \over {\color{orange}2}a}\]

\[x = {-b \pm \sqrt{b^2-{\color{orange}3}ac} \over {\color{orange}3}a}\]

...but you may not know that it can be extended to the quartic, quintic and beyond:

\[x = {-b \pm \sqrt{b^2-{\color{orange}{8 \over 3}}ac} \over {\color{orange}4}a}\]

\[x = {-b \pm \sqrt{b^2-{\color{orange}{5 \over 2}}ac} \over {\color{orange}5}a}\]

In the next section, I'll show how to generalize the quadratic by applying Pascal's Triangle diagonals to its insides.

Demo Link: General Quadratic (desmos)

The formula

\(d_{eg}=2\)    (...3 extracts cubic extrema; 4 quartic inflex, 5...)

\(\frac{-b\pm\sqrt{b^{2}-\frac{2d_{eg}}{d_{eg}-1}ac}}{d_{eg}a}\) works at any degree other than 1.

---

WIP: Description / how to use it at any degree

Demo Link: General Cubic (desmos)

The formula

\(d_{eg}=3\)    (...4 extracts quartic extrema; 5 quintic inflex...)

\(i_{nbit}=\left(\frac{-1}{d_{eg}^{3}}\right)\frac{b^{3}}{a^{3}}+\left(\frac{3}{d_{eg}^{2}\left(

d_{eg}-1\right)}\right)\frac{bc}{a^{2}}+\left(\frac{-3}{d_{eg}\left(d_{eg}-1\right)\left(d_{eg}-2\right)}\right)\frac{d}{a}\)

\(d_{iscrim}=i_{nbit}^{2}+\left(\left(\frac{-1}{d_{eg}^{2}}\right)\frac{b^{2}}{a^{2}}+\left(\frac{2}{d_{eg}\left(d_{eg}-1\right)}\right)\frac{c}{a}\right)^{3}\)

\(c_{ubic}=\sum_{n=0}^{1}\sqrt[3]{i_{nbit}+\left(-1\right)^{n}\sqrt{d_{iscrim}}}-\frac{b}{d_{eg}a}\)

* Notice how Pascal's (Inverted) Triangle diagonals [-1, 3, -3, omit] and [-1, 2, omit] and [possibly the 1 on \(-\frac{b}{d_{eg}a}\)] appear in the numerators of the generalized cubic equation. Similar truncated diagonals seem to also appear in the general quadratic.
* TODO: Show surpise derivation of cubic equation after locator move.
* Ask readers if the patterns seen here / quadratic could simplify the quartic equation.

The formula

TODO: ... can we simplify and generalize the quartic equation based on what we see above?